Analisis Deret Waktu

Data deret waktu ialah data yang dikumpulkan pada suatu kurun waktu. Misalkan data penjualan bulanan yang dikumpulkan dari tahun 1999-2000. Atau data pengukuran produksi pabrik X setiap hari dalam kurun waktu Jan 2005 – Mar 2005.

Suatu data deret waktu dapat dipengaruhi oleh 1 faktor atau kombinasi 4 faktor di bawah ini yaitu :

1. Faktor Trend (T)
2. Faktor Siklus (Cyclical=C)
3. Faktor Musiman (Seasonal=S)
4. Faktor Acak (Random=R, atau Irregular=I)

Gambar 1 –> data deret waktu dipengaruhi oleh faktor Tren (T) dan Siklus (C)

Gambar 2 –> data deret waktu dipengaruhi oleh faktor Siklus (C)

Gambar 3 –> data deret waktu dipengaruhi oleh faktor Musiman (S) dan Tren (T)

Gambar 4 –> data deret waktu dipengaruhi oleh faktor Musiman (S), Tren (T), Siklus (C), dan faktor acak (R)

Untuk menentukan Trend suatu data deret waktu dapat digunakan beberapa cara, misalnya : Metode Tangan Bebas (Freehand Method), Metode Rataan Semi (Semi Average), Metode Rataan Bergerak (Moving Average), Metode Kuadrat Terkecil (Least Square Method)

Analisis Regresi Linier Berganda

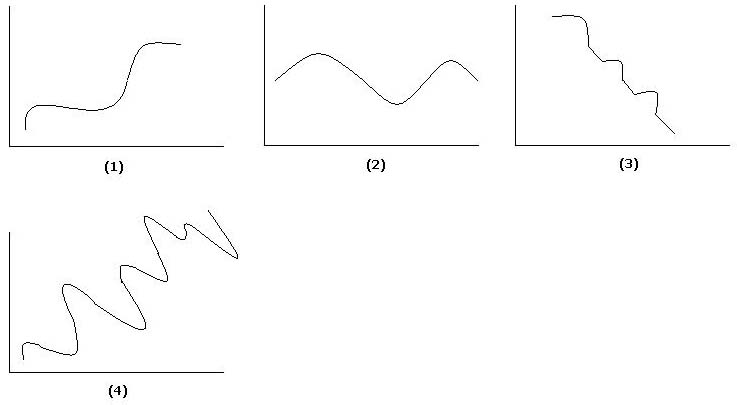
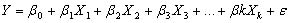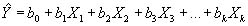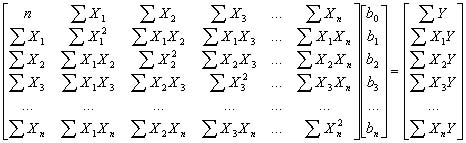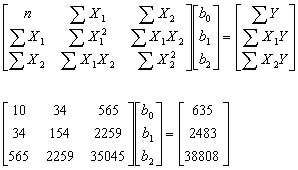Analisis regresi linier berganda ialah suatu alat analisis dalam ilmu statistik yang berguna untuk mengukur hubungan matematis antara lebih dari 2 peubah.Bentuk umum persamaan regresi linier berganda ialah sebagai berikut :

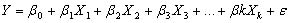
Persamaan tersebut diduga oleh persamaan di bawah ini :

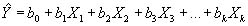
Menentukan b₀, b₁, b₂, …, b_k dapat menggunakan metode kuadrat terkecil melalui apa yang disebut dengan persamaan normal seperti di bawah ini :

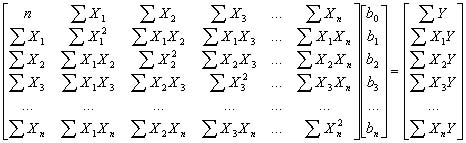
Bentuk persamaan matriks di atas termasuk ke dalam suatu sistem persamaan linier.Mencari atau menentukan b₀, b₁, b₂, b₃, …, b_n berarti mencari atau menentukan solusi dari sistem persamaan linier (SPL).Mencari solusi SPL ada berbagai macam cara, diantaranya ialah Metode Eliminasi Gauss, Metode Invers (Metode Matriks yang diperbesar dan Metode Matriks Adjoin), dan Metode Cramer.

Metode Cramer merupakan metode yang paling populer dalam menentukan suatu solusi SPL karena sifatnya yang mudah dipelajari dan sederhana.Menurut Cramer jika kita punya SPL sebagai berikut :

Maka x₁, x₂, x₃, …, x_n dapat langsung dicari dengan membagi determinan matriks A_j dengan determinan matriks koefisien A.Dimana :

 

Teladan :

Diketahui peubah nilai ekonomi makro (Y) dipengaruhi oleh jumlah jam belajar per minggu (X₁) dan nilai pengantar ekonomi (X₂) dengan data sebagai berikut :

 

MahasiswaYX1X2

140130

244135

349242

453247

560350

665362

769464

878571

985679

1092785

 

Berdasarkan data di atas tentukan hubungan matematis antara nilai ekonomi makro dengan jumlah jam belajar per minggu dan nilai pengantar ekonomi.

Jawaban :

Dari data di atas diketahui bahwa Y merupakan fungsi linier dari X₁ dan X₂, Y=f(X₁, X₂) sehingga persamaan regresi yang didapat akan seperti ini :

Y = b₀ + b₁X₁ + b₂X₂

Mahasiswa	Y	X1	X2	X1.X1	X2.X2	X1.X2	X1.Y	X2.Y
1	40	1	30	1	900	30	40	1200
2	44	1	35	1	1225	35	44	1540
3	49	2	42	4	1764	84	98	2058
4	53	2	47	4	2209	94	106	2491
5	60	3	50	9	2500	150	180	3000
6	65	3	62	9	3844	186	195	4030
7	69	4	64	16	4096	256	276	4416
8	78	5	71	25	5041	355	390	5538
9	85	6	79	36	6241	474	510	6715
10	92	7	85	49	7225	595	644	7820
Jumlah (Σ)	635	34	565	154	35045	2259	2483	38808

Persamaan normalnya ialah sebagai berikut :

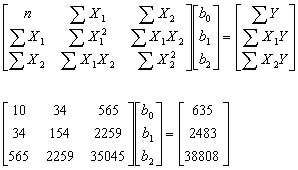
Dengan metode Cramer didapatkan b₀ = 20.638; b₁=3.742; b₂=0.533 sehingga persamaan regresinya menjadi :

Y = 20.638 + 3.742 X₁ + 0.533 X₂