Analisis Regresi Linier Berganda
Analisis regresi linier berganda ialah suatu alat analisis dalam ilmu statistik yang berguna untuk mengukur hubungan matematis antara lebih dari 2 peubah.Bentuk umum persamaan regresi linier berganda ialah sebagai berikut :
Persamaan tersebut diduga oleh persamaan di bawah ini :
Menentukan b0, b1, b2, …, bk dapat menggunakan metode kuadrat terkecil melalui apa yang disebut dengan persamaan normal seperti di bawah ini :
Bentuk persamaan matriks di atas termasuk ke dalam suatu sistem persamaan linier.Mencari atau menentukan b0, b1, b2, b3, …, bn berarti mencari atau menentukan solusi dari sistem persamaan linier (SPL).Mencari solusi SPL ada berbagai macam cara, diantaranya ialah Metode Eliminasi Gauss, Metode Invers (Metode Matriks yang diperbesar dan Metode Matriks Adjoin), dan Metode Cramer.
Metode Cramer merupakan metode yang paling populer dalam menentukan suatu solusi SPL karena sifatnya yang mudah dipelajari dan sederhana.Menurut Cramer jika kita punya SPL sebagai berikut :
Maka x1, x2, x3, …, xn dapat langsung dicari dengan membagi determinan matriks Aj dengan determinan matriks koefisien A.Dimana :
Teladan :
Diketahui peubah nilai ekonomi makro (Y) dipengaruhi oleh jumlah jam belajar per minggu (X1) dan nilai pengantar ekonomi (X2) dengan data sebagai berikut :
MahasiswaYX1X2
140130
244135
349242
453247
560350
665362
769464
878571
985679
1092785
Berdasarkan data di atas tentukan hubungan matematis antara nilai ekonomi makro dengan jumlah jam belajar per minggu dan nilai pengantar ekonomi.
Jawaban :
Dari data di atas diketahui bahwa Y merupakan fungsi linier dari X1 dan X2, Y=f(X1, X2) sehingga persamaan regresi yang didapat akan seperti ini :
Y = b0 + b1X1 + b2X2
|
Mahasiswa |
Y |
X1 |
X2 |
X1.X1 |
X2.X2 |
X1.X2 |
X1.Y |
X2.Y |
|
1 |
40 |
1 |
30 |
1 |
900 |
30 |
40 |
1200 |
|
2 |
44 |
1 |
35 |
1 |
1225 |
35 |
44 |
1540 |
|
3 |
49 |
2 |
42 |
4 |
1764 |
84 |
98 |
2058 |
|
4 |
53 |
2 |
47 |
4 |
2209 |
94 |
106 |
2491 |
|
5 |
60 |
3 |
50 |
9 |
2500 |
150 |
180 |
3000 |
|
6 |
65 |
3 |
62 |
9 |
3844 |
186 |
195 |
4030 |
|
7 |
69 |
4 |
64 |
16 |
4096 |
256 |
276 |
4416 |
|
8 |
78 |
5 |
71 |
25 |
5041 |
355 |
390 |
5538 |
|
9 |
85 |
6 |
79 |
36 |
6241 |
474 |
510 |
6715 |
|
10 |
92 |
7 |
85 |
49 |
7225 |
595 |
644 |
7820 |
|
Jumlah (Σ) |
635 |
34 |
565 |
154 |
35045 |
2259 |
2483 |
38808 |
Persamaan normalnya ialah sebagai berikut :
Dengan metode Cramer didapatkan b0 = 20.638; b1=3.742; b2=0.533 sehingga persamaan regresinya menjadi :
Y = 20.638 + 3.742 X1 + 0.533 X2

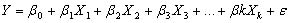

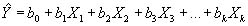

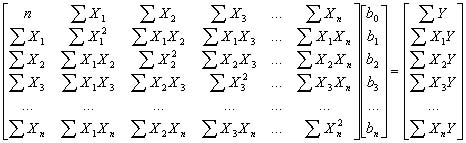





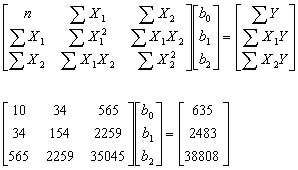


saptyawan — December 13, 2008 @ 5:43 am
trims banget, saya sudah cari kemana-mana disini baru ketemu pencerahannya.ok
tarista — December 23, 2008 @ 10:55 am
Matur nuwun…terima kasih banyak infor anda bermanfaat. Tapi dapatkah saya diberi tahu cara membuat program untuk matrik dengan metode creamer. Syukur2 klo dalam PHP. Makasih
admin — December 24, 2008 @ 9:57 pm
@Saptyawan : senang bisa membantu anda
@tarista : terima kasih kembali, tentang matrix sy masih susun programnya, tetapi jika anda familiar dengan excel, ada situs bagus yang membahas operasi matriks dengan ms. excel, silahkan klik juniadi chaniago di Friends Everywhere
nonkha ayu monica — January 8, 2009 @ 7:12 pm
saya mau tanya.regresi linier berganda apa sama dengan metode permukaan respon???trima kasih.
admin — January 9, 2009 @ 10:53 pm
@Nonkha : Regresi linier berganda berbeda dengan metode respon permukaan (surface response method). Metode respon permukaan merupakan salah satu pemodelan stokastik dimana salah satu prosedurnya dapat menggunakan regresi linier melalui metode kuadrat terkecil. Jika anda tertarik dapat membaca jurnal Biometrics 1954;10:16-60 tulisan Box dan Wilson judulnya ‘The Exploration and Exploitation of response surface’
ayu — January 13, 2009 @ 2:38 pm
saya mw tanya,, bs tlg jelaskan apa yang dimaksud forward selection??
tlg dijelaskan mpe tuntas coz susah bgt dicari bahannya,,
thx b4
admin — January 14, 2009 @ 12:24 am
@Ayu : Forward Selection merupakan salah satu metode pemodelan (pembangunan model linier) untuk menemukan kombinasi peubah yang “terbaik” dari suatu gugus peubah. Secara umum pada stepwise regression ada dua macam cara pembangunan model liniernya yaitu Backward Selection dan Forward Selection. Untuk mudahnya kita lihat contoh berikut : Misalkan ada 1 peubah Y (peubah terikat) dan 7 peubah X (X1, X2, X3,…,X7 peubah bebas). Untuk menentukan atau mencari model hubungan linier antara peubah terikat dengan peubah bebasnya dapat dilakukan metode stepwise regresion menggunakan forward sel. atau backward.
Backward : Masukan seluruh peubah ke dalam persamaan sehingga modelnya ialah Y = Konstanta + X1 + X2 + X3 + X4 + X5 + X6 + X7, kemudian satu persatu peubahnya dikurangi sedemikian hingga kriteria tertentu dipenuhi.
Forward : Persamaan dimulai dari nol peubah, kemudian satu persatu peubah dimasukan sampai kriteria tertentu dipenuhi. Peubah X mana saja yang dimasukan ? Pertama-tama tetapkan nilai p patokan (terserah berapa nilainya, biasanya 0.10, atau 0.15). Misalkan p patokan = 0.10. Kemudian lakukan regresi sederhana Y dengan X1, lihat nilai p-nya. Y dengan X2, lihat nilai p-nya, dst sampai dengan Y dengan X7. Peubah X yang dimasukan ke persamaan ialah X yang nilai-P nya dibawah P patokan kita. Seandainya yang nilai p-nya dibawah ialah X1, X3, dan X5 maka persamaannya ialah Y=Konst+X1+X3+X5… Semoga cukup jelas :thumbsup:
wahyu — February 3, 2009 @ 2:34 pm
saya mau tanya, bagaimana cara mencari F table dan T table???
terima kasih.
admin — February 5, 2009 @ 2:06 pm
@wahyu : mencari f table dan t table dapat dilihat di lampiran2 buku teks statistik, program statistik atau dapat pula menggunakan microsoft excel. Jika menggunakan Excel untuk mencari F tabel ketikan =FINV(alpha, db1, db2) dimana alpha ialah nilai taraf nyata yang diinginkan, db ialah derajat bebas. Untuk T tabel ketikan =TINV(alpha, db). Contoh : =FINV(0.05, 1, 12)
=TINV(0.05, 12)
dhicky — April 15, 2009 @ 1:20 pm
saya mau tanya.
bagaimana mencari b1 dan b2 dlm regresi berganda secara manual.
utk matriks di atas saya sdh lupa cara menghitungnya.
apakah ada cara lain, klo ada tolong jelaskan?
admin — April 18, 2009 @ 6:41 pm
@dhicky : bo, b1, dan b2 dapat dicari dengan memecahkan 3 persamaan liniernya. Sebagai contoh kita gunakan data nilai mahasiswa di atas : persamaan yang kita dapatkan ialah sebagai berikut :
pers. 1 –> 10 b0 + 34 b1 + 565 b2 = 635
pers. 2 –> 34 b0 + 154 b1 + 2269 b2 = 2483
pers. 3 –> 565 b0 + 2269 b1 + 35045 b2 = 38808
Substitusikan pers. 1 dan pers. 2 untuk mereduksi 1 peubah bebas(hasilnya misal pers. 4 yang hanya mengandung dua peubah bebas). Kemudian substitusikan pers. 2 dan pers.3 untuk mereduksi 1 peubah (hasilnya misal pers 5 yang hanya mengandung 2 peubah). Terakhir substitusikan pers. 4 dengan pers. 5. Dengan cara demikian akan didapatkan nilai bo, b1, dan b2. Cukup jelas ?
ike — April 23, 2009 @ 6:22 pm
kalau pada tabel analisis variansi untuk menguji subset (k-p)BETAs, itu lo mengidentufikasi x1 yang dianggap berpengaruh dengan x2 yg dianggap tidak berpengaruh setelah x1. cara mencari jumlah kuadratnya gimana ya?
apa bedanya rumus jumlah kuadrat x yg sendiri2 dg setelah dipengaruhi yang lain. jangan pakai matrik ya!
nurdiana — May 26, 2009 @ 12:56 pm
saya mau tanya apa kegunaan dari variabel kontrol dalam hipotesa, lalu apakah setiap satu variabel dalam penelitian minimal harus terdiri dari 30 sampel?? skripsi saya mempunyai 6 variabel tahun penelitian hanya 1 tahun dan menggunakan 48 sampel.jika seperti ini apakah saya harus menggunakan 30×6 variabel= 180 sampel.
rian — May 28, 2009 @ 10:54 am
apa makna atau cara membaca persamaan regresi Y = 2,455 + 0,196X1 + 0,271X2 + 0,245X3 + e
admin — May 28, 2009 @ 8:59 pm
@rian : untuk membaca suatu pers. regresi perlu diuji dulu parameter regresi dugaannya menggunakan uji F dan uji t. Jika diasumsikan uji F dan telah dilakukan maka pers. di atas artinya :
– perubahan X1 sebesar 1 satuan akan menyebabkan perubahan Y sebesar 0.196 satuan
– perubahan X2 sebesar 1 satuan akan menyebabkan perubahan Y sebesar 0.271 satuan
– perubahan X3 sebesar 1 satuan akan menyebabkan perubahan Y sebesar 0.245 satuan
admin — May 28, 2009 @ 10:15 pm
@nurdiana : secara umum ukuran sample > 30 mencukupi. Cukup banyak sebetulnya pro cons masalah ukuran sample 30 tetapi sebagian besar pro. Untuk masalah anda jika 6 variable tersebut diambil datanya dari sample sama maka ukuran sample 48 yang anda pakai cukup memadai.
Rudy — May 29, 2009 @ 5:22 am
dari persamaan regresi yang didapat, apa artinya konstanata? Bagimana cara membaca konstanta tersebut.
admin — May 30, 2009 @ 8:33 pm
@Rudy : Konstanta menunjukan nilai awal (initial) untuk peubah terikat (Y) manakala peubah bebasnya (X) nol semua. Kita misalkan persamaan regresi Y = 2 + 3X1 + 2X2 ; Angka 2 di atas adalah konstanta. Pada saat X1=0 dan X2=0 maka Y = 2 atau sama dengan konstantanya.
resta — June 8, 2009 @ 10:33 am
saya mo tanya tentangkelebihan regresi probit dibandingkan regresi logistik?
admin — June 8, 2009 @ 11:07 pm
@resta : keduanya hampir sama (dilihat dari bentuk kurvanya), jika kedua bentuk regresi tersebut diterapkan pada gugus data yang sama maka akan menghasilkan penduga koefisien yang hampir sama. Menurut Aldrich dan Nelson (1984) perbedaannya hanya dari faktor proporsionalitas dengan besar kira2 1.8
Didit — June 11, 2009 @ 8:02 am
saya maw tanya apakah regresi linier berganda sama dengan korelasi berganda?
admin — June 12, 2009 @ 12:59 am
@didit : korelasi mengukur derajat keeratan hubungan antara peubah, sedangkan regresi mengukur hubungan antara peubah bebas dan terikatnya dalam bentuk persamaan linier
Didit — June 13, 2009 @ 5:36 pm
maw tanya donk..
klo hasil persamaannya 35.291,183 + 3,99X1 + 281,162X2 itu bisa ga c??
ap hasil b1 dan b2 harus dibawah 1 nilainya??
makasih yaaah
admin — June 13, 2009 @ 8:45 pm
@didit: selama prosesnya benar (sampling, input data, asumsi dipenuhi) maka hasilnya bernilai. Namun demikian interpretasi hasil persamaan regresi dikembalikan kepada si peneliti, apakah mempunyai arti secara praktis atau tidak.
Didit — June 13, 2009 @ 11:30 pm
makasi yaah..
satu lagi niii..
waktu saat mengeliminasi, boleh tidak kita membagi nilai tersebut..
contohnya
pers. 1 –> 10 b0 + 34 b1 + 565 b2 = 635
pers. 2 –> 34 b0 + 154 b1 + 2269 b2 = 2483
pers. 3 –> 565 b0 + 2269 b1 + 35045 b2 = 38808
misalkan semua persamaan dibagi 10 semua..
biar nilai b0 pada persamaan menjadi 1..
boleh ga?
makasi..
admin — June 14, 2009 @ 5:09 am
@didit : boleh, itu salah satu dari 3 operasi baris elementer (baca pendahuluan)
olin — December 6, 2009 @ 7:25 pm
mau tanya donk
gimana nyari data untuk masalah analisis regresi sederhana dan analisis regresi berganda???thx b4
Sukma — December 22, 2009 @ 6:37 pm
dari contoh diatas bagaimana mencari standard error nya ?
admin — December 28, 2009 @ 8:40 pm
@ Olin : Data sangat berlimpah di internet, coba saja salah satu statistics link di web ini. Untuk regresi yang penting datanya memiliki hubungan sebab akibat, berskala nisbah (baca pendahuluan), dan memenuhi asumsi-asumsi yang mendasarinya.
admin — December 28, 2009 @ 8:45 pm
@sukma : menghitung JKG (Jumlah Kuadrat Galat) atau SSE (Sum Square Error) jika dilakukan secara manual memerlukan waktu. Lebih mudah anda melakukan perintah regression di SPSS atau regress di minitab maka SSE akan muncul di window output.
kiki — February 12, 2010 @ 8:52 pm
boleh taw ga aQu bisa dapet contoh skripsi atau ekonomi keuangna yang menggunakan Backward Selection dan Forward Selection???atau buku yang membahas Backward Selection dan Forward Selection ????
admin — February 15, 2010 @ 11:15 am
@kiki : Yang paling praktis dapat dilihat di manual SPSS atau SAS, disitu dibahas lengkap tentang metode backward dan forward selection.
Ali \ Dudut — February 22, 2010 @ 3:55 pm
haduh.. puyeng aku..
ridho — March 14, 2010 @ 8:43 pm
terima kasih banget gan…akhirnya w menemukan apa yang wa cari..terus berkreasi…
budi — March 26, 2010 @ 6:28 am
makasiiiii…dapet pencerahan dari sini…
mudi — April 8, 2010 @ 11:12 am
maw tanya nih, saya lagi buat skripsi tentang pengaruh profesionalisme auditor terhadap materialitas. dan setelah diuji degan uji t maka muncullah persamaan regresi Y=34.60 + 0.914×1 + 0.340×2 + 0.225×3 + 0.523×4 + 0.254×5 + e
saya udah coba buat nerangin ke dosen bimbingan tapi dia bilang kliru,trus q jadi tambah bingung ni maunya gmn, tolong dikasih tau cara membacanya ya..
amel — June 2, 2010 @ 3:27 pm
mo tnya nichh..
nilai b0 tu dpt dr mn sichh…
tlg jawab yachh…
makasih
inge — June 22, 2010 @ 8:48 am
mw nanya nii….KL kontanta d Regresi Liner Berganda – (minus) artinya apa…?
contoh : -0,777+0,281 X1+0,174 X2+ 0,037 X3 – 0,061 X4
Rudi — August 27, 2010 @ 6:33 pm
sy mau tanya nih. bagaimana jika kita membangun odel regresi (RLB) dengan data time series? apakah kita perlu untuk menguji stasioneritas data var bebas dan terikatnya?
Buku2 yang ada hanya menjelaskan data time series pada analisis peramalan (AR, MA, ARMA, ARIMA). untuk model tersebut dikatakan bahwa apabila tidak stasioner maka akan menyebabkan spouriuos regression. bagaimana jika yang dibangun hanya RLB biasa? Thanx
HAMKA — February 11, 2011 @ 6:37 pm
MAU NANYA PEMBIMBIM SAYA SELALU MENAYAKAN BERAPA NILAI y DARI PERSAMAAN REGRESI, JADI SEBELUM MENGETAHUI NILAI X KATANYA UDAH HARUS TAU DULU NILAI Y NYA MOHON PENJELASANNYA
yunie — March 14, 2011 @ 8:42 pm
mu tanya donk,,,wat laporan kp saya kan menggunakan regresi trus ma dosen aku ditanyain konsep regresinya aku bilang kan mencari pengaruh variabel prediktor thdp respon.
kata dosen saya salah yg bener tu mencari prediksi.
yang bener gmn sie?maksud dosen gmn aku ga ngerti.
nabila damayanti — May 21, 2011 @ 3:50 pm
bisa kasih contoh dengan menggunakan data rill ?
saya ada tugas kuliah, mencari data ril dari BI, BPS, BEI, atau yg lain.
mohon bantuannya.
terima kasih
retno — May 23, 2011 @ 6:51 am
mau tanya ni langkah2nyari koefisien regresi berganda yang lewat matriks dengan software minitab gmn y?
tyara — May 31, 2011 @ 11:13 pm
mau tanya nih, klo mau cari regresi dengan cara konstanta nya sama dg nol bagaimana yah ?
emriadi — June 2, 2011 @ 8:49 pm
terima kasih atas informasi nya……salam kenal
emriadi — June 3, 2011 @ 3:54 pm
terima kasih ini bermanfaa…..salam kenal
asiah — June 5, 2011 @ 12:13 pm
cara invers matriks gmna???
lavigne — June 14, 2011 @ 12:38 am
mw ty donk knapa klau menggunakan data responden/data primer harus menggunakan log dalam regresi linier berganda?
wid — June 17, 2011 @ 8:28 am
mau tny nih…lengkapnya tentang backward selection bs dicari dmn sih….
Bintoro Halim — September 16, 2011 @ 10:56 am
Mau tanya donk bagaimana interpretasi nih persamaan??
1. Loyalty = – 11.014 + 0.873 X1+ 0.722 X2 + 0.813 X3
2. Satisfaction = 8.676 + 0.578 X4 – 0.337 X5
3. Trust = 21.557 – 0.615 X5 + 0.843 X6
merly — September 17, 2011 @ 1:22 pm
persamaan regresi linear berganda penelitian saya sbb : Y=-0.964 – 0.015X1 + 0,279X2 + 0,153X3 + 0,508X4 apakah persamaan regresi ini salah??? dan bagaimana menginterprestasikannya? mhn bantuannya, terimakasih
yunita — October 11, 2011 @ 2:31 pm
kalo analisis regresi berganda dgn 2 var bebas n 1 var.moderasi rumusnya gmn ya?
yuin — November 10, 2011 @ 12:04 pm
mau tanya,,
beda analisis regresi linier berganda dengan regresi dua prediktor apa ya?
rumus dr masing2 analisis tsb sprti ap?
terus beda variabel bebas dan tergantung dengan prediktor dan kriterium apa?
terimakasih .. =)
rozi — November 29, 2011 @ 12:26 pm
Assalamualaikum, mas saya mau tanya, cara penghitungan metrik dengan metode cremer gimana ya mas, soalnya saya masih belum paham contoh yang ada di atas. terimakasih sebelumnya
iyandri — December 20, 2011 @ 8:52 am
wduh cramer apa itu ya ??
fahmi — December 24, 2011 @ 8:21 pm
Numpang tanya.
Apakah ada materi RSM yang bisa dibuat bahan belajar? TKs
anak statistik — January 11, 2012 @ 9:05 pm
maaf numpang tanya, klo regresi itu stuan dr tiap variable independen nya hrus sama apa tidak? klo harus, adakah cara untuk mnyamakan satuanya trsbut? trimakasih
yuin — February 1, 2012 @ 8:41 am
tanya donkkkk…
beda analisis linier berganda dengan analisis dua prediktor dan analisis regresi berganda apa?
beda kriterium dan prediktor dengan bebas dan tergantung apa?
umi — February 13, 2012 @ 12:37 pm
nanya,,ada yg tau tarik menarik garis regresi??
stevani — February 20, 2012 @ 4:01 pm
sya mau tnyk mas,
arti standart error dalam persamaan regresi linier berganda apa?
trus ad ngak hubungannya dengan nilai konstanta di persamaan itu?
mhn bantuanny
tq 🙂
joni — March 7, 2012 @ 10:07 pm
dimana saya bisa membaca tinjauan pustaka tentang metode permukaan response dan cara penentuan plot optimum beserta titik2 nya..?
mohon penejelasannya
diah — April 10, 2012 @ 3:08 pm
mau tanya dong..
bagaimana jika variabel bebas x1 dan x2 memiliki hubungan (korelasi). apakah solusi2 yg telah anda sebutkan diatas bisa menjelaskannya?
putri — May 7, 2012 @ 12:47 pm
kalau variabelnya dummy yaitu 1 0 , dan ada 6 buah X nya…
bagaimana?
aam fitria — May 15, 2012 @ 7:24 pm
Mau tanya donk. .
Perbedaan reg.logit n probit kan ada pada data, klo normal pakek probit kalo gag normal pakek logit, trus normal kenapa gag pakek reg.linier? Apa keunggulan probit dr reg.linier?? Makassiii. . .
bahri — July 29, 2012 @ 7:53 am
mw nax nich,,,
aq lg terkendala di perhitungan regresi linear berganda. saya punya judul yg menggunakan regresi berganda Variabel bebasnya ada 2, sy bingung cara untuk menghitung,, apalagi klo mesti pake manual…
ada ngak tutorial yg dihitung mengggunakan exel supaya bisa mempermuada perhitungan…
klo ada minta tlg donk di kirim ke email saya,,
bahrimalker@yahoo.co.id
lina — August 19, 2012 @ 5:59 pm
aslm,,maaf boleh minta rumus mencari regresi berganda secara manual gak tapi bukn dengan matriks??? mksih,,,
ridho — September 27, 2012 @ 10:03 am
izin bertanya.,.,
saya mau meneliti hubungan antara beberapa parameter kualitas perairan (yang sling berhubungan jga satu-sama lain)terhadap kepadatan dan persebaran populasi biota jenis A di perairan,.,.,
tepatkah menggunakan metode Regresi linear berganda ini..??
mohon bantuan dan rekomendasinya…
wahyuwati — October 31, 2012 @ 9:29 am
apa sih kelebihan antara respon permukaan dibandingkan dengan metode regresi?
SisiL — November 5, 2012 @ 3:01 pm
Tanya dong..
penelitian saya menggunakan regresi berganda dengan dua variabel kontrol..var.kontrol tersebut saat pengujian diperlakukan seperti var.independen.mengapa begitu??
Mohon bantuannya..trimakasi
ferry — May 12, 2013 @ 8:29 pm
gmna cra membuat error kehomogenan,,,,, eror kenormaln n error kebebasan y
aff — October 26, 2013 @ 7:59 pm
ass.. numpng nanyak,,, analisis data yang tepat buat menghitung perbandingan misal.x menghitung pengaruh motivasi dan minat belajar yang tepat itu apakah lbih baik menggunakan regresi linear ganda atau menggunakan anilisis data bukan-t
admin — October 31, 2013 @ 8:55 am
@ aff : Coba gunakan analisis korelasi
kadafi — November 9, 2013 @ 9:24 am
mas mau tanya nih misalkan kan mas meneliti : X1 : jumlah jam per minggu? X2 : Pengantar Ilmu Ekonomi ?
nah misalkan ada peneliti B yang meneliti X1 : Pengantar ilmu Ekonomi dan X2 : Jumlah jam perminggu? persamaan regresinya berbeda kan mas pasti?
tetapi kenapa hasil dari regresinya juga berbeda mas? ketika saya inputkan misal X1 =10 dan X2 = 20 pada hasil yang didapatkan oleh mas. Dan X1 = 20 dan X2 = 10 pada hasil yang didapatkan pada penganalisa B?
2. Bagaimana cara menentukan berdasarkan data yang kita ambil di lapangan bahwa data itu X1, X2 dan atau seterusnya …?
Mohon pencerhannya terimakasih
admin — November 10, 2013 @ 9:07 pm
@semua : mohon maaf baru saya bisa ol lagi setelah sekian lama karena ada permasalahan teknis dengan blog ini sehingga baru bisa saya tanggapi komentarnya.
@kadafi : Y disebut peubah terikat sedangkan X (X1, X2, dst) disebut peubah bebas. Dalam kasus di atas, seandainya X1 dan X2 ditukar tidak menjadi masalah, persamaanya akan memberikan hasil yg sama (bisa anda coba). Persamaan akan berubah jika peubah bebasnya ditukar dengan peubah terikatnya. Penentuan apakah peubah yang kita teliti peubah bebas atau terikat salahsatunya bisa dilihat dengan menentukan yang mana sebab yang mana akibat (atau hasil). Peubah hasil biasanya peubah terikat : seperti contoh di atas bahwa nilai ditentukan oleh jumlah jam belajar.
elyza — January 20, 2014 @ 9:06 am
saya mau tanya kalau variabel x nya ada 3 bagaimana?
akbp wahyu bintoro — September 8, 2017 @ 4:10 pm
I feel this is among the so much important info for me. And i’m satisfied reading your article.
But want to statement on few basic things, The website taste is wonderful, the articles is
in reality great : D. Good process, cheers
Gali Subastian — November 2, 2017 @ 8:35 am
Pak, ada gak perhitungan manual koefisien regresi untuk masalah data panel Model Fixed Effect dgn Dummy Variabel ?? terima kasih mohon Balasannya
Dian enjelin — January 4, 2018 @ 5:44 pm
Mau nanya… kalo
Kan di contoh soal persamaannya cuman sampai x2,kalau sampai x4 mau mencari b4 nya… persamaan nya gimana ya… mohon bantuannya…
rifaldi siregar — January 7, 2018 @ 12:18 pm
nilai b0 nya darimana itu gan