Analisis Korelasi Linier Sederhana

Analisis di atas digunakan untuk mengukur derajat keeratan hubungan antara dua peubah. Bilangan yang mengukur kekuatan hubungan antara dua peubah disebut dengan koefisien korelasi ( r ). Koefisien korelasi memiliki nilai antara -1 sampai dengan 1. r = 1 artinya hubungan antara X dan Y kuat dan searah (positif) ; r = -1 artinya hubungan antara X dan Y kuat dan berlawanan arah (negatif) ; r = 0 artinya hubungan antara X dan Y lemah atau hubungan antara X dan Y bukan hubungan yang linier.

Sebelum dapat melakukan analisis korelasi linier sederhana diperlukan syarat-syarat atau asumsi sebagai berikut :

1. Terdapat hubungan logika antara peubah yang akan dikorelasikan
2. Skala peubah sekurang-kurangnya skala selang (interval)
3. Terdapat studi awal (penelitian, referensi, jurnal, pustaka, dll) yang menunjukan indikasi hubungan antara 2 peubah yang akan dikorelasikan *

Syarat nomor 3 di atas merupakan opsional, jika penelitian mengenai hubungan antara peubah yang dikorelasikan belum pernah dilakukan sebelumnya.

Koefisien korelasi pearson ( r ) didapatkan dari rumus sebagai berikut :

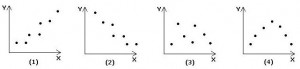
Untuk melihat hubungan antara peubah x dan y secara grafik digunakan diagram pencar (scatter diagram). Secara umum hubungan antara dua peubah dapat berupa bentuk seperti gambar di bawah ini :

Gambar (1) menunjukan hubungan antara peubah X dan peubah Y kuat dan searah (positif), ditandai oleh nilai r yang mendekati 1

Gambar (2) menunjukan hubungan antara peubah X dan peubah Y kuat dan berlawanan arah (negatif), ditandai oleh nilai r yang mendekati -1

Gambar (3) menunjukan hubungan antara peubah X dan peubah Y yang lemah, ditandai oleh nilai r yang mendekati 0

Gambar (4) menunjukan hubungan antara peubah X dan peubah Y yang bukan linier, ditandai oleh nilai r yang mendekati 1

Untuk nilai-nilai r antara 0 dan 1 dengan 0 dan -1 tidak ada patokan pasti yang menentukan batas kekuatan hubungan antara 2 peubah. Namun demikian dapat digunakan konvensi sebagai berikut :

Hubungan antara peubah X dan Y disebut kuat dan searah jika 0.75 ≤ r ≤ 1.

Hubungan antara peubah X dan Y disebut kuat dan berlawanan arah jika -1 ≤ r ≤ -0.75.

Hubungan antara peubah X dan Y disebut lemah jika -0.75 < r < 0.75.

Jika r dikuadratkan maka akan didapatkan suatu nilai yang disebut dengan koefisien determinasi. Koefisien determinasi menunjukkan seberapa besar pengaruh satu peubah terhadap peubah lainnya.

Misal r² = a maka artinya :

–> a x 100% keragaman dalam nilai-nilai Y dapat dijelaskan oleh hubungan liniernya dengan X.

–> sumbangan peubah X terhadap naik turunnya Y ialah a x 100%

Teladan :

Diketahui 2 peubah X dan Y sebagai berikut :

Tentukan kekuatan hubungan antara kedua peubah di atas, dan tentukan pula besar pengaruh satu peubah terhadap peubah lainnya.

Jawaban :

r² = 0,90

–> Hubungan antara peubah X dan Y kuat dan positif

–> 90% keragaman dalam nilai-nilai Y dapat dijelaskan oleh hubungan liniernya dengan X

1 Comment

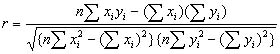
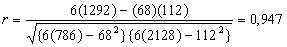
1. Gunz_ — April 27, 2009 @ 9:28 pm

   Thanks, buat posting’n materi2’y…

RSS feed for comments on this post. TrackBack URI

Leave a comment